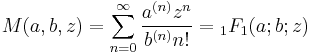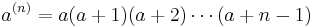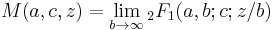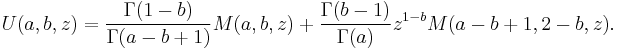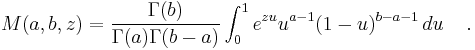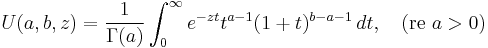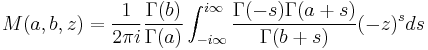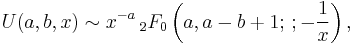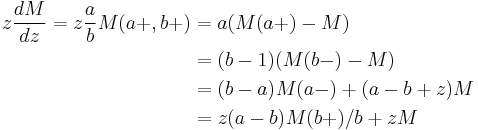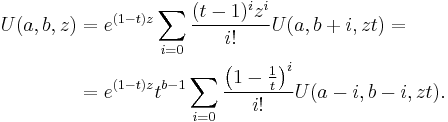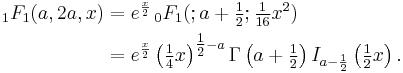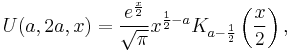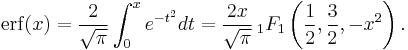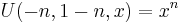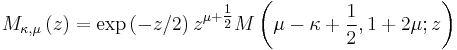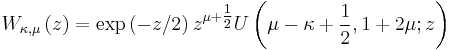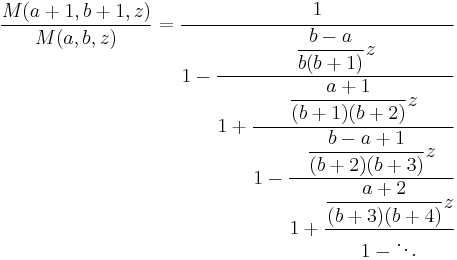Confluent hypergeometric function

In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity. (The term "confluent" refers to the merging of singular points of families of differential equations; "confluere" is Latin for "to flow together".) There are several common standard forms of confluent hypergeometric functions:

The Kummer functions, Whittaker functions, and Coulomb wave functions are essentially the same, and differ from each other only by elementary functions and change of variables.

Contents

Kummer's equation

Kummer's equation is

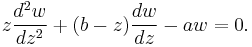z\frac{d^2w}{dz^2} %2B (b-z)\frac{dw}{dz} - aw = 0.\,\!,

with a regular singular point at 0 and an irregular singular point at ∞. It has two linearly independent solutions M(a,b,z) and U(a,b,z).

Kummer's function (of the first kind) M is a generalized hypergeometric series introduced in (Kummer 1837), given by

M(a,b,z)=\sum_{n=0}^\infty \frac {a^{(n)} z^n} {b^{(n)} n!}={}_1F_1(a;b;z)

where

a^{(n)}=a(a%2B1)(a%2B2)\cdots(a%2Bn-1)\,

is the rising factorial. Another common notation for this solution is Φ(a,b,z). This defines an entire function of a.b, and z, except for poles at b = 0, −1, − 2, ...

Just as the confluent differential equation is a limit of the hypergeometric differential equation as the singular point at 1 is moved towards the singular point at ∞, the confluent hypergeometric function can be given as a limit of the hypergeometric function

M(a,c,z) = \lim_{b\rightarrow\infty}{}_2F_1(a,b;c;z/b)

and many of the properties of the confluent hypergeometric function are limiting cases of properties of the hypergeometric function.

Another solution of Kummer's equation is the Tricomi confluent hypergeometric function U(a;b;z) introduced by Francesco Tricomi (1947), and sometimes denoted by Ψ(a;b;.z). The function U is defined in terms of Kummer's function M by

U(a,b,z)=\frac{\Gamma(1-b)}{\Gamma(a-b%2B1)}M(a,b,z)%2B\frac{\Gamma(b-1)}{\Gamma(a)}z^{1-b}M(a-b%2B1,2-b,z).

This is undefined for integer b, but can be extended to integer b by continuity.

Integral representations

If Re b > Re a > 0, M(a,b,z) can be represented as an integral

M(a,b,z)= \frac{\Gamma(b)}{\Gamma(a)\Gamma(b-a)}\int_0^1 e^{zu}u^{a-1}(1-u)^{b-a-1}\,du\,\quad .

For a with positive real part U can be obtained by the Laplace integral

U(a,b,z) = \frac{1}{\Gamma(a)}\int_0^\infty e^{-zt}t^{a-1}(1%2Bt)^{b-a-1}\,dt, \quad (\operatorname{re}\ a>0)

The integral defines a solution in the right half-plane re z > 0.

They can also be represented as Barnes integrals

M(a,b,z) = \frac{1}{2\pi i}\frac{\Gamma(b)}{\Gamma(a)}\int_{-i\infty}^{i\infty} \frac{\Gamma(-s)\Gamma(a%2Bs)}{\Gamma(b%2Bs)}(-z)^sds

where the contour passes to one side of the poles of Γ(−s) and to the other side of the poles of Γ(a+s).

Asymptotic behavior

The asymptotic behavior of U(a,b,z) as z → ∞ can be deduced from the integral representations. If z = x is real, then making a change of variables in the integral followed by expanding the binomial series and integrating it formally term by term gives rise to an asymptotic series expansion, valid as x → ∞:[1]

U(a,b,x)\sim x^{-a} \, _2F_0\left(a,a-b%2B1;\,�;-\frac 1 x\right),

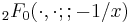where _2F_0(\cdot, \cdot;�;-1/x) is a generalized hypergeometric series, which converges nowhere but exists as a formal power series in 1/x.

Relations

There are many relations between Kummer functions for various arguments and their derivatives. This section gives a few typical examples.

Contiguous relations

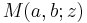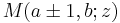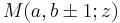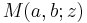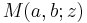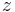Given \displaystyle M(a,b;z), the four functions \displaystyle M(a\pm 1,b;z), \displaystyle M(a,b\pm 1;z) are called contiguous to \displaystyle M(a,b;z). The function \displaystyle M(a,b;z) can be written as a linear combination of any two of its contiguous functions, with rational coefficients in terms of a,b and z. This gives (4
2)=6 relations, given by identifying any two lines on the right hand side of

\begin{align} z\frac{dM}{dz} = z\frac{a}{b}M(a%2B,b%2B) &=a(M(a%2B)-M)\\ &=(b-1)(M(b-)-M)\\ &=(b-a)M(a-)%2B(a-b%2Bz)M\\ &=z(a-b)M(b%2B)/b %2BzM\\ \end{align}

In the notation above, 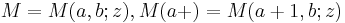\displaystyle{}M= {}M(a,b;z), M(a%2B)={}M(a%2B1,b;z) and so on.

Repeatedly applying these relations gives a linear relation between any three functions of the form 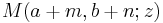\displaystyle{}M (a%2Bm,b%2Bn;z) (and their higher derivatives), where m, n are integers.

There are similar relations for U.

Kummer's transformation

Kummer's functions are also related by Kummer's transformations:

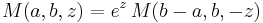
M(a,b,z) = e^z\,M(b-a,b,-z)
U(a,b,z)=z^{1-b} U\left(1%2Ba-b,2-b,z\right).

Multiplication theorem

The following multiplication theorems hold true:

\begin{align}U(a,b,z)&= e^{(1-t)z} \sum_{i=0} \frac{(t-1)^i z^i}{i!} U(a,b%2Bi,z t)=\\ &= e^{(1-t)z} t^{b-1} \sum_{i=0} \frac{\left(1-\frac 1 t\right)^i}{i!} U(a-i,b-i,z t).\end{align}

Connection with Laguerre polynomials and similar representations

In terms of Laguerre polynomials, Kummer's functions have several expansions, for example

M\left(a,b,\frac{x y}{x-1}\right) = (1-x)^a \cdot \sum_n\frac{a^{(n)}}{b^{(n)}}L_n^{(b-1)}(y)x^n (Erdelyi 1953, 6.12)

Special cases

Functions that can be expressed as special cases of the confluent hypergeometric function include:

For example, the special case b= 2 a the function reduces to a Bessel function:

\begin{align}\, _1F_1(a,2a,x)&= e^{\frac x 2}\, _0F_1 (; a%2B\tfrac{1}{2}; \tfrac{1}{16}x^2) \\ &= e^{\frac x 2} \left(\tfrac{1}{4}x\right)^{\tfrac{1}{2}-a} \Gamma\left(a%2B\tfrac{1}{2}\right) I_{a-\frac 1 2}\left(\tfrac{1}{2}x\right).\end{align}

This identity is sometimes also referred to as Kummer's second transformation. Similarly

U(a,2a,x)= \frac{e^\frac x 2}{\sqrt \pi} x^{\frac 1 2 -a} K_{a-\frac 1 2} \left(\frac x 2 \right),

where K is related to Bessel polynomial for integer a.

\mathrm{erf}(x)= \frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2} dt= \frac{2x}{\sqrt{\pi}}\,_1F_1\left(\frac{1}{2},\frac{3}{2},-x^2\right).
U(-n,1-n,x)= x^n\,
M_{\kappa,\mu}\left(z\right) = \exp\left(-z/2\right)z^{\mu%2B\tfrac{1}{2}}M\left(\mu-\kappa%2B\frac{1}{2}, 1%2B2\mu; z\right)
W_{\kappa,\mu}\left(z\right) = \exp\left(-z/2\right)z^{\mu%2B\tfrac{1}{2}}U\left(\mu-\kappa%2B\frac{1}{2}, 1%2B2\mu; z\right)
\operatorname{E} \left[\left|N\left(\mu, \sigma^2 \right)\right|^p \right]= \left(2 \sigma^2\right)^\frac p 2 \frac {\Gamma\left(\frac{1%2Bp}2\right)}{\sqrt \pi}\, _1F_1\left(-\frac p 2, \frac 1 2, -\frac{\mu^2}{2 \sigma^2}\right),
\operatorname{E} \left[N\left(\mu, \sigma^2 \right)^p \right]=(-2 \sigma^2)^\frac p 2 \cdot U\left(-\frac p 2, \frac 1 2, -\frac{\mu^2}{2 \sigma^2} \right) (the function's second branch cut can be chosen by multiplying with (-1)^p).

Application to continued fractions

By applying a limiting argument to Gauss's continued fraction it can be shown that

\frac{M(a%2B1,b%2B1,z)}{M(a,b,z)} = \cfrac{1}{1 - \cfrac{{\displaystyle\frac{b-a}{b(b%2B1)}z}} {1 %2B \cfrac{{\displaystyle\frac{a%2B1}{(b%2B1)(b%2B2)}z}} {1 - \cfrac{{\displaystyle\frac{b-a%2B1}{(b%2B2)(b%2B3)}z}} {1 %2B \cfrac{{\displaystyle\frac{a%2B2}{(b%2B3)(b%2B4)}z}}{1 - \ddots}}}}}

and that this continued fraction converges uniformly to a meromorphic function of z in every bounded domain that does not include a pole.

Notes

  1. ^ Andrews, G.E.; Askey, R.; Roy, R. (2000). Special functions. Cambridge University Press .

References

External links